目次
数学
定義とかメモ
スカラーとテンソル
- スカラー<html><p>ベクトル空間とは別物として定義されている.だいたい実数.
スカラー乗法という演算が定義できる.ベクトル空間は任意の体で定義できるので,本来は任意の体の元であればよい.</p></html>物差しという意味のスケーラーと同じ.
線形空間でないものの例,$r$と$\phi$を元とするやつ.
- ユークリッド空間
- デカルト座標系
- テンソル
- 行列
数であれば何でもスカラーというわけではないし,行列で書ければ何でもテンソルというわけでもない. スカラーは座標変換に対して変化しない量のこと.つまり,ベクトルの中身の元はスカラーとは言わない.
別の定義として,「テンソルとはふたつのベクトルを入力としてスカラーを出力するもの」とも考えられる.
定義域
関数 $f$ の定義域は ${\rm dom} f$ と表す.
値域
${\rm codom} f$
集合
演算
- 二項演算 $f: X \times X \rightarrow X$
$f(a,b)$や$ab$と表記することもある
性質
- 結合法則 $(ab)c=a(bc)$
- 交換法則 $ab=ba$
- 分配法則 加法 $+$ と乗法 $\cdot$ が定義されていて
$a\cdot (b+c)=a\cdot b+a\cdot c$かつ$(a+b)\cdot c=a\cdot b+a\cdot c$
| 群 | group | 演算 $\cdot$ がある.単位元 $e$ がある.逆元がある. |
| 可換群(アーベル群) | commutative group / abelian group | 演算 $\cdot$ がある.単位元 $e$ がある.逆元がある.演算 $\cdot$ に交換法則. |
| 環 | ring | TODO |
| 体 | field | TODO |
微積
- リーマン積分(縦分割的) ↔ ルベーグ積分(横分割的)
線形代数
| 用語 | 数式 | 常に出来る | 対角になる | 相似性の保存 |
|---|---|---|---|---|
| 対角化 | $A=PDP^\top$ | x | o | o |
| 固有値分解 | $A=PDP^\top$ | x | o | o |
| 特異値分解 | $A=UDV^\top$ | o | o | x |
| ジョルダン標準形 | $A=PJP^\top$ | 条件付きo | x | o |
そのうち書く
- 行列の基本変形
- 主成分
簡約化
行列の基本変形を何度か施して以下を満たす行列にすること
- 行ベクトルのうち零ベクトルは零ベクトルでないものより下の行にある
- 零ベクトルでない行の主成分は1である
- $i$行目の行ベクトルの主成分が$j_i$列目にあったとすると$j_1 < j_2 < j_3 < \dots $
- 各行の主成分を含む列の他の成分はすべて0
例) $$ \left[ \begin{array}{ccccc} 0 & 1 & 3 & 0 & 2\\ 0 & 0 & 0 & 1 & 1\\ 0 & 0 & 0 & 0 & 0 \end{array} \right] $$ 1行目の主成分は2列目,2行目の主成分は4列目であるから正しい順番になっている. またこれら主成分のある列は主成分以外0であるので正しい.
階数(ランク)
ある行列$\bf A$のランク${\rm rank}({\bf A})$は $\bf A$の簡約化$\bf B$の零ベクトルでない行の数である.
微分
対角行列
ベクトル $\boldsymbol{v}=[v_1 \; v_2 \; \dots v_n]$ を対角行列にしたもの ${\rm diag}(\boldsymbol{v})$ は以下のようになる. $$ {\rm diag}(\boldsymbol{v}) = \left(\begin{array}{cccc} v_1 & & & 0\\ & v_2 & & \\ & & \ddots & \\ 0 & & & v_n \end{array}\right) $$
線形空間(ベクトル空間)
線形空間 = ベクトル空間
$V$が線形空間であるとは
- 加算と定数倍が定義されている
- 任意の$u,v \in V$に対して$u+v\in V$
- 任意の$v\in V$とスカラー$k$に対して$kv\in V$
スカラーが集合$K$のとき,K上の線形空間という.
擬似逆行列
pseudo inverse matrix
共分散行列の図形的意味
- 2つある固有ベクトルはプロットをガウス分布と考えた時の主成分のベクトル
- 固有値はベクトルの長さ?
幾何
幾何(geometry)は変換(transformation)と空間(space)の数学である.
『幾何学とは,ある変換のもとで不変な図形の性質を研究する学問である』
by エルランゲン・プログラム(クライン) ← クラインの壺で有名
「空と海の出会うところは どれほど遠いの」
⇒ ユークリッド幾何では平行線は絶対に出会わない
⇒ ユークリッドではない新たな幾何学(射影幾何学)の導入
- 射影空間
- ユークリッド空間 + 無限望遠
- 無限遠点
- 無限遠直線
- 無限遠平面
幾何学
ユークリッド幾何学 < 計量のある幾何学 < アフィン幾何学 < 射影幾何学
変換
| 鏡映・スキュー | 拡大・縮小 | 回転 | 平行移動 | |
|---|---|---|---|---|
| 射影変換 | o | o | o | o |
| アフィン変換 | o | o | o | o |
| 相似変換 | x | o | o | o |
| 線形変換 | o | o | o | x |
| ユークリッド変換 | x | x | o | o |
スキュー(skewing) = せん断(shearing) : 長方形を平行四辺形にするような変換
射影変換(projective transformation = homography transformation)
射影 = 投影
射影幾何メモ
| great circle | 大円 | 球面上で,球の中心を通るような円 つまり球面と,球の中心をとおる平面の交差する円状の線 |
二次元ユークリッド空間を同次座標系で表した空間を考える. これは三次元空間である. ここでは二次元ユークリッド空間上のある点は直線として表される. $(kx,ky,k)$ で表される.つまり二次元ユークリッド空間上の全ての点は, 同次座標系では原点をとおる直線である. 二次元ユークリッド空間上の全ての点を同次座標系での直線として表現し,同次空間上の単位球と交差させてみる. 全ての点は単位球と2つの交点を持っているはず(しかも球の真反対側に). つまり,この単位球をどこの方角から見ても全ての二次元ユークリッド空間中の点が見えるということ. なので,この同次座標系空間を適当にぶった切る平面には全ての二次元ユークリッド空間上の点が乗るはずである.(原点をとおる直線と交差するから)
さらに,この同次座標系空間をぶった切る平面として $w=1$ つまり通常の二次元ユークリッド空間といえる平面を選ぶ. すると,無限遠点というのはその平面側から単位球を見て,ちょうど輪郭に当たる部分(大円)に散りばめられているはずである. 無限遠点の性質として常に $w=0$ となる点であることが考えられる. これはつまり地球で言うところの赤道のこと.
二次元ユークリッド空間を同次座標系で表したユークリッド平面がある. このユークリッド平面上の二つの平行線を単位球に投影すると, 無限遠点はともにxy平面上に投影され,単位球の大円となる.
同じように二次元ユークリッド空間上の直線、つまり点の集合を, 同次座標系上の単位円に投影してみると大円になるし,実体としては同次座標系空間中で平面である. つまり,二次元ユークリッド空間での直線は同次座標系空間での平面である.
平面が直線であることから重要なことがわかる. 無限遠点を単位球に投影したら赤道にあることから, 無限遠点は単位球と $w=0$ 平面との交差する場所であり, つまり平面をなすので,二次元ユークリッド空間上では直線状に並んでいると言えるのだ. これ(赤道)を無限遠直線と呼んでいる.
2
行列が正則でないとき,変換後は何らかの情報が失われてしまい, 復元が不可能となる.つまり,逆行列は存在しない. いくつかの違うベクトルが同じ元に写像されてしまうのだ.
円錐の断面は楕円(Ellipse),放物線(Parabola)または双曲線(Hyperbola)となる. これら3つは二次曲線として知られる. 放物線は円錐の母線に平行な断面のとき. (厳密に言えば円錐の側面のある点pから中心に向かう直線に対して垂直かつ点pを通る母線に平行.)
交差判定
Multiple View Geometry 参考
二次元
二点を通る直線について
${\bf l} = {\bf x}_1 \times {\bf x}_2$
交差判定について
直線は ${\bf l} = (a,b,c)^\top$ として表す.
この直線は $ax+by+c=0$ を満たす.
$k\neq 0$ を使って ${\bf l} = k (a,b,c)^\top$ と表しても良い.
つまり,定数倍に対して同じものである.
この式は $(x,y,1)$ を用いて $(x,y,1)(a,b,c)^\top=0$ とも表現できる. 座標に関しても,これは同時座標なので $k\neq 0$ を使って $(kx,ky,k)$ と表せる.
さて二つの直線の交点 ${\bf x}$ だがこれは外積 $\times$ を使って簡単に表せる.
${\bf x} = {\bf l}_1 \times {\bf l}_2$
同次座標系なので最後の要素で全てを割ることで詳細な数値が分かる.
これを使えば ${\bf l}$ に定数が掛けられていようが無視できる. 無限遠で交差する場合(平行のとき)は同次座標の最終要素が0となっている.
メモ
確率
尤度関数と確率密度関数は別物
尤度関数は尤もらしさを表す.確率密度関数は定義域で積分すると1となるが,
尤度関数は必ずしもそうではない.
たとえば,裏表の出る確率が異なるコインがあって,2回投げて2回表が出たとき,
そのコインの表が出る確率pは1が尤もらしい.
2回投げて1回表が出たら0.5が尤もらしい.
尤度関数は$p(表の観測回数=x|表が出る確率=\theta)$ だが,
定義域$\theta$で積分すると1にはならないことがわかる.
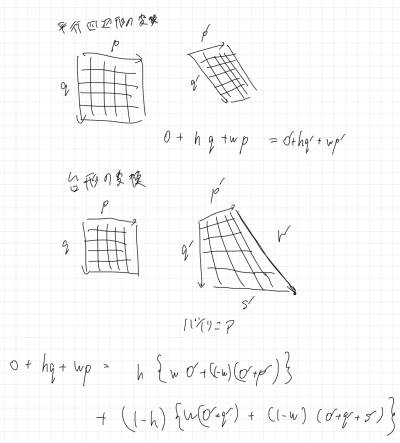
EMDとWasserstein距離
EMD(Earth Mover Distance)は離散のとき.Wasserstein Distanceは連続のとき.
最適輸送問題とも言われる.ある土(Earth)が分布していたときに,
目的の形に地形を整える場合,どこからどういうふうに土を運ぶのが最も仕事量が少ないかを計算する.
Binary Cross Entropy
事象が二つの離散確率分布 $p$ と $q$ がある。
交差エントロピーの定義から $$H(p,q) = E_p[-\log q] = \sum_{x\in \{0,1\}} \left( -p(x) \log q(x) \right) = -p(0) \log q(0) - p(1) \log q(1) $$
分布 $p$ のほうを正解とすると、
半端な値ではなく、二値のどちらかが正解となるので、
$p(0)=0, p(1)=1$ となるか $p(0)=1, p(1)=0$ となる。
したがって $H(p,q)$ は $-\log q(0)$ または $-\log q(1)$ となる。
分布 $q$ のほうはニューラルネットの出力値である。
分布の和が $1$ であることから $q(0) = 1-q(1)$ の関係にある。
なので結局 $H(p,q)$ は $-\log (1- q(1))$ または $-\log q(1)$ になることとなる。
ここで $p=0$ を $p(0)=1, p(1)=0$ のこととし、
$p=1$ を $p(0)=0, p(1)=1$ のこととする。
同様に$q=0$ を $q(0)=1, q(1)=0$ のこととし、
$q=1$ を $q(0)=0, q(1)=1$ のこととする。
こうすると $H(p,q) = - (1-p) \log (1-q) - p \log q $ となり、
${\rm bce}(q,0) = -\log(1-q)$ 、 ${\rm bce}(q,1) = -\log(q)$ と一致する。
Cross Entropy
本来の交差エントロピーは離散確率変数のとき $$ H(p,q) = -\sum_x p(x) \log q(x) $$ である。 結合エントロピーでも $H(p,q)$ という表記になるので注意(別物)。
最適化
| optimal point | 最適点 (最適解となる点) |